Hola,
Hoy (y los próximos días) vamos a ver unas cosas asombrosas, pero que han sido siempre así, aunque la mayoría no lo sepa.
Todos los lenguajes de programación son imperfectos en cierto sentido.
1.-Tenemos una memoria finita.
2.-Los tipos de datos numéricos están limitados.
3.-Nuestros programitas quieren hacer uso de números no limitados.
Esto hace que explorando los límites obtengamos resultados inesperados.
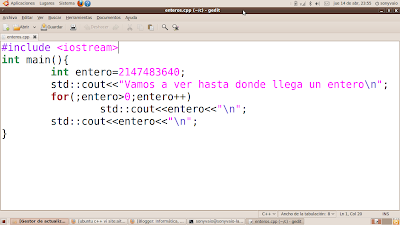
EJEMPLO EN C++:
1.-Normalmente los tipos int (enteros) son de 4 bytes (32 bits).
2.-Si elegimos utilizar un entero con signo (para representar números negativos y positivos) podremos representar este rango:
Desde -2^31 hasta 2^31-1
O lo que es lo mismo:
Desde -2.147.483.648 hasta 2.147.483.647
3.-La representación interna es en complemento a dos.
¿Cómo son los números positivos en complemento a dos?
Los positivos son como siempre:
5 en decimal = 0000 0101 en binario.
¿Cómo son los números negativos en complemento a dos?
Se invierten los 0-s y 1-s (realmente sería sumar un 1 a todos los dígitos ya que 1+1 es 0 igual que 6+4=0 al hacer una suma decimal sin tener en cuenta la llevada).
y después de la inversión se suma un 1.
4 en decimal = 0000 0100
complemento de 4: 1111 1011
complemento más suma: 1111 1100
¿Y la gran ventaja?
Por ejemplo la resta 5 – 4 = 1 se hace por medio de una suma:
0000 0101 + 1111 1100 = 0000 0001
¡Magia!
¿y qué pasa cuando llegamos al límite de los 4 bytes?
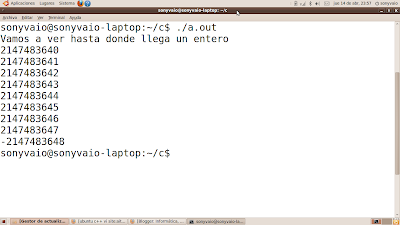
supongamos que en nuestro programa numero = 2.147.483.646
hacemos numero++ y obtenemos 2.147.483.647 que es exactamente el límite que hemos indicado antes (2^31-1).
Ahora que estamos en el límite hacemos numero++ y…
nos da -2.147483648.
Explicación:
2.147.483.647 en decimal es 0111 1111 1111…………………….1111 en binario.
Recordad que en complemento a dos que el primer dígito sea 0 indica que es un número positivo.
Ahora bien, al sumar un uno obtenemos (¡¡¡Ahora es un número negativo!!!)
1000 0000 0000……………………………………..0000
-2.147.483.648 en complemento a dos.
La prueba: