He tratado de mostrar que el algoritmo eficiente para el problema dado.
1] Cómo averiguar el número máximo en una matriz?
# include
int main () {
int a [20] = {0}, i, n, BIG;
printf («Introduzca el tamaño de la matriz n»); scanf
(«% d», & n);
printf («Introduzca la matriz Elementos n»);
for (i = 0; i
Cómo averiguar el número mínimo de una matriz?
# include
int main () {
int a [20 ] = {0}, i, n, PEQUEÑO,
printf («Introduzca el tamaño de la matriz n»);
scanf («% d», & n );
printf («Introduzca la matriz Elementos n»);
for (i = 0; i
(o) Una lógica más se puede utilizar para averiguar el número de minutos en un array
# include
int ()
principal {
int a [20] = {0}, i, n, PEQUEÑO,
printf («Introduzca el Tamaño de matriz n «);
scanf («% d «, & n);
printf (» Introduzca la matriz Elementos n «);
for (i = 0; i
/ * Intialise la variable PEQUEÑA a 0 * /
PEQUEÑO = 0;
for (i = 1, i
PEQUEÑO = i;}
printf («El valor de Número MIN en array es:% d n», a [SMALL]);
}
Cómo averiguar el segundo número mínimo de una matriz
Hay varias maneras de averiguar el segundo número mínimo
1. mediante ordenamiento de burbuja ordenar los elementos en orden ascendente y para averiguar el valor mínimo y su complejidad es O (n ^ 2)
2. Hay otra forma de implementar con la complejidad de O (n), por favor, encontrar la sa me a continuación.
# include
int main () {
int a [20] = {0} i, n, primero, segundo,
printf («Introduzca el tamaño de la matriz n»);
scanf («% d» , y n);
printf («Introduzca la matriz Elementos n»);
for (i = 0; i
/> / * 1. Intialise la variable PEQUEÑA a 0 * /
primero = segundo = 32767 / * INT_MAX VALOR * /;
for (i = 0; i
/ * Si el número actual es menor que primero
continuación, actualice primero y segundo * /
if (a [i]
segundo = primero;
primero = a [i];}
/ * Si el número actual está entre primero y segundo
luego actualizar segundos * /
más {
if ((a [i]
}
if (segundos == 32767) />
}
else {printf />
============================= =====
¿Cuál es la clasificación?
medios elementos en un orden determinado (ascendente / descendente) pueden organizar la clasificación.
Hay muchos factores a considerar antes de elegir el mejor algoritmo.
1. Tiempo complejidad -> ¿Cuánto tiempo el algoritmo tarda en completar
2.. Complejidad espacial -> la cantidad de memoria de trabajo (normalmente RAM) es necesario por el algoritmo. Esto tiene dos aspectos: la cantidad de memoria que necesita el código y la cantidad de memoria necesaria para los datos sobre los que opera el código. Elige el mejor algoritmo de clasificación basado en la complejidad,
complejidad representa generalmente en BIG-O-notación O (n), O (n ^ 2), etc.
1] algoritmo Bubble Sort: (Orden ascendente) (O ( n ^ 2))
Esta es la simple algoritmo. Mejor y peor escenario complejidad temporal de este algoritmo O (n ^ 2). Este algoritmo se puede mejorar y lograr una mejor complejidad del caso como O (n).
# include
int /> () {
int a [20] = {0}, i, j, temp, n;
printf («Introduzca el tamaño de la matriz n»);
scanf («% d», & n);
printf («Introduzca la matriz Elementos n») ;
for (i = 0; i
for (i = 0; i
for (j = 0; j
{
si (a [j]> a [j +1])
; {
temp = a [j];
a [j] = a [j +1];
un [ j +1] = temp;
}
}
}
para ( i = 0; i
1] Mejora Ordenar algoritmo burbuja: (Orden ascendente) (O (n))
; # include
int main () {
int a [20] = {0}, i, j, temp, n, intercambiado,
printf />
scanf («% d», & n);
printf (» Introduzca la matriz Elementos n «);
for (i = 0; i
intercambiado = 1; / / set cambió a 1 para iniciar la primera pasada
/ * Ist Loop (bucle principal) * /
/ * si la bandera se convierte en 0 y luego se detiene de clasificación * /
for (i = 0; ((i
{
intercambiado = 0;
/ * Segundo Loop * /
for (j = 0; j
; temp = a [j];
a [j] = a [ j +1];
una [j +1] = temp;
/ * class=»com»> Indica que se ha producido un intercambio. * /
class=»com»>
}}
}
for (i = 0; i
compatible 2] Selección Ordenar Algoritmo: (Orden ascendente) (O (n ^ 2))
# include
int main () {
int a [20] = {0}, i, j, temp, n, index_min;
printf />
scanf («% d», & n);
printf (» Introduzca la matriz Elementos n «);
for (i = 0; i
/ * averiguar el Índice * /
Min / * Ist Loop (Principal Loop) * /
for (i = 0; i
; for (j = i; j
index_min = j;
}
/ * swap de los valores * /
temp = a [i];
a [i] = a [index_min];
un [index_min] = temp;
}
for (i = 0; i
compatible 2] algoritmo de ordenación rápida: (Orden ascendente) (O (n log n))
rápida especie es un divide y vencerás algoritmo.
Tiene dos fases 1. fase de la partición 2. Clasificación fase
pivot_item = partición (array, bajo, alto) -> O (n)
quick_sort (a, bajo, pivote-1) -> T (n / 2) quick_sort />
T (n / 2) => O (n) + T (n / 2) + T (n / 2) = O (n log n)
purple;»> Si matriz sólo contiene un elemento, el retorno
Else
elegir un elemento para utilizar como pivote
elementos partición en dos subconjuntos:.
Elementos menor o igual a pivotar
Elementos mayores de pivote
; QuickSort dos subconjuntos
resultados de Retorno
# include
/ *
* partition_array ()
* /
int partition_array (int a [], int bajo, int alto)
{int pivote, izquierda, derecha, temp;
; izquierda = baja;
derecha = alta;
pivote = a [bajo];
while (izquierda
}
/ / Move right mientras artículo> pivote
mientras que (a [derecha]> pivote)
{
derecha -;
}
if (izquierda
un [right] = temp;
}}
/ / derecha es la posición final para el
un pivote [bajo ] = a [derecha],
un [right] = pivote;
regresar derecha;}
/ *
* Quick Ordenar
* /
void quicksort (int a [], int bajo, int alto)
{int pivot_item;
/ / Terminación
if (Mayor> Menor)
{
= pivot_item partition_array (a, bajo, alto);
printf (» pivot_item:% d n «, pivot_item);
/ * Lado izquierdo ordenar los elementos Traverse antes Pivot_item * /
quicksort (. a, bajo, pivot_item-1);
/ * Lado derecho ordenan los elementos Traverse Después Pivot_item * /
quicksort (a, pivot_item 1, alto);
}}
int main () {
int a [20] = {0}, i, j, temp, n, index_min;
printf («Introduzca el tamaño de la matriz n ‘); scanf
(» % d «, & n);
printf (» Introduzca la matriz Elementos n «);
for (i = 0; i
/ * Paso 1: * /
/ * Averigüe el elemento pivote utilizando partición * /
/ * Clasificar los elementos utilizando recursividad * /
3] Merge sort Algoritmo: (Orden ascendente) (O (n log n))
Merge ordenación se basa en dividir y conquistar algoritmo
El algoritmo mergesort es tan sigue; su ejecución se ilustra de la siguiente manera:
- Si la secuencia de entrada tiene un solo elemento, volver.
- Partición de la secuencia de entrada en dos mitades.
- Clasificar los dos subsecuencias utilizando el mismo algoritmo.
- Combinar las dos subsecuencias ordenadas para formar la secuencia de salida
- MERGE-SORT ( Array, bajo , de alta )
1. SI bajo < alto / / Comprobar si el caso base
2. ENTONCES mediados = ( bajo + high)/2] / / Divide paso
3. MERGE-SORT (Array, bajo , mediados ) / / Conquer paso.
4. MERGE-SORT (Array, ;. mitad + 1 , alta ) / / Conquer paso
5. ; MERGE (Array, bajo , mediados , alta ) / / Combinar paso.
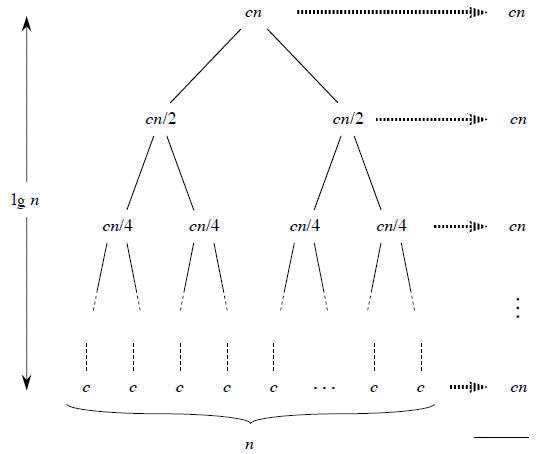 -.> cn lg n + cn
-.> cn lg n + cn
ignorando término de orden inferior cn y constantes coefciente c , y tenemos,
/ *
* merge_sorted_arrays ()
* /
int merge_sorted_arrays (int a [], int bajo, int mediados, int alto)
{int i = Baja; / * Seguimiento de primera gama * /
int j = centro 1; / * Seguimiento de segunda matriz * /
int indice = 0; / * array temp pista * /
/ * array temporal se requiere * /
int temp [50], k;
while ( (i <= centro) && (j <= alto))
{if (a [i] <= a [j ]) {
temp [index] = a [i];
; i + +;}
else {
temp [index] = a [j]; />
}
;
}
while (i <= centro)
{
temp [index] = a [i];
index + +;
i + +;}
while (j <= alto)
{ ; temp [index] = a [j];
index + +; />
;}
/ / Copiar el arreglo temporal en que la matriz principal
for (k = 0; k <índice; k + +)
{
una [k + baja] = temp [k];
}
}
/ *
* Combinar Sort -> array parition utilizando recursividad
* /
vacío partition_array (int a [], int bajo, int alto)
{
int mediados;
/ / Terminación
si (bajo alta <)
{ mid = (bajo + alto) / 2;
/ * Divida el array hasta mediados de * /
partition_array ( a, baja, media ),
/ * Divida la matriz a partir de mediados de 1 * /
partition_array ( a, mediados 1, de alta ),
/ * Combinar las dos matrices ordenadas en una matriz. * /
merge_sorted_arrays (a, bajo, medio, alto);
}}
/ *
* Principal ()
* /
int main () {
int a [20] = {0}, i, j, n,
printf («Introduzca el tamaño de la matriz n «);
scanf («% d «, & n);
printf (» Introduzca la matriz Elementos n «);
for (i = 0; i
/ * Combinar Ordenar * /
partition_array (a, 0, n-1);
for (i = 0; i
Para Animación de Merge Ordenar: http://littlesnailworkshop.blogspot.in/2012 / 07/technique-merge-sort-animation.html

