A partir de ser vivo en la raíz, tal árbol se ramifican a los mamíferos, aves, vida marina, etc />
Árbol como estructura de datos
Un árbol es una estructura de datos que se hace de los nodos y enlaces, como una lista enlazada. La diferencia entre ellos radica en la forma en que se organizan.
- El nodo superior del árbol se llama el root y todos los demás nodos se ramifican desde ésta
- Cada nodo del árbol puede tener cierta cantidad de
. Cada nodo hijo puede a su vez ser el nodo padre a sus hijos, etc. - nodos hijos pueden tener vínculos sólo a partir de un solo padre
- Cualquier nodo más alto que el padre se llama antepasado nodo.
- nodos que no tienen hijos son llamados hojas (nodo hoja)
- Cualquier nodo que no es ni una raíz, ni una hoja se denomina nodo interior
- La altura de un árbol se define como el longitud de la ruta más larga de la raíz a una hoja i n ese árbol (incluida la ruta raíz)
Un interno nodo (también conocido como un nodo interno, inode para abreviar, o nodo rama) es cualquier nodo de un árbol que tiene nodos secundarios. Del mismo modo, un nodo externo (también conocido como un nodo exterior, nodo hoja o nodo terminal) es cualquier nodo que no tiene hijos nodos.
Binary Tree
Así, cada nodo puede tener ningún niño, un niño o dos niños.
Los punteros nos ayudan a identificar si se trata de un hijo de la izquierda o un niño bien.
(o)
Aplicación de un árbol binario
Antes de definir cualquier algoritmo formales, echemos un vistazo a una posible aplicación de un árbol binario
Considere un conjunto de números:. 25,63,13, 72,18,32,59,67.
Supongamos que guardamos estos números en los nodos individuales de una lista enlazada. Para buscar un elemento en particular, tenemos que ir a través de la lista, y tal vez hemos Togo hasta el final de la lista también. Por lo tanto si había un número n, nuestra complejidad búsqueda sería O (n).
¿Es porque los números no están en ningún orden determinado? Ahora supongamos que orden los siguientes números:
13,18,25,32,59,63,67,72. y almacenarlos en otra lista enlazada.
¿Cuál sería la complejidad búsqueda ahora? Es posible que se sorprenda al descubrir que todavía es O (n) .
Simplemente no se puede aplicar de búsqueda binaria en una lista enlazada con O (log n) complejidad. Usted todavía tiene que ir
través de cada enlace para localizar un número determinado. Así que una estructura ligada lineal no nos está ayudando en absoluto.
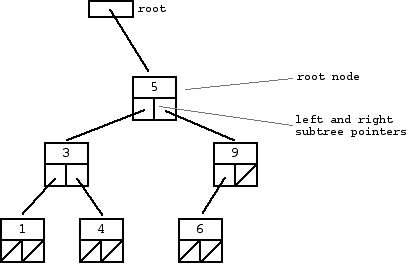
El árbol que se muestra más arriba es un árbol binario de búsqueda – el nodo «raíz» es un 5, y sus nodos subárbol izquierdo (1, 3, 4) son <= 5, y sus nodos subárbol derecho (6, 9) son> 5. De forma recursiva, cada uno de los subárboles también debe obedecer las restricciones árbol de búsqueda binaria: en el (1, 3, 4) sub árbol, el 3 es la raíz, el 1 <= 3 y 4> 3. Ten cuidado con la redacción exacta de los problemas – un «árbol binario de búsqueda» es diferente de un «árbol binario».
Los nodos en el borde inferior del árbol tienen subárboles vacíos y se llaman nodos «hoja» (1, 4, 6), mientras que los otros son nodos «internos» (3, 5, 9).
Tree Terminologías
Longitud de una ruta de acceso: La longitud de un camino es el número de nodos en el camino
El grado de un nodo es el número de aristas conectadas al nodo .
o ¿Cuántos nodos secundarios están conectados a ese nodo